[Python] 약수의 개수와 덧셈 (프로그래머스)

문제를 보시려면 클릭하세요

문제 설명

두 정수 left와 right가 매개변수로 주어집니다. left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주세요.

제한 사항

1 ≤ left ≤ right ≤ 1,000

입출력 예

---

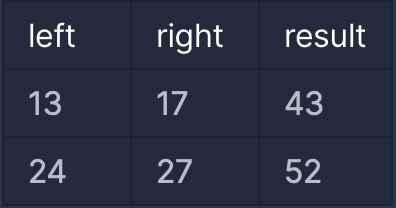나의 코드

def solution(left, right):
    result = 0
    for i in range(left, right + 1):
        result += dividor(i)
    return result

def dividor(n):
    result = len([i for i in range(1, n+1) if not n%i])
    return -n if result%2 else n

다른 사람의 더 짧은 코드

def solution(left, right):
    answer = 0
    for i in range(left,right+1):
        if int(i**0.5)==i**0.5:
            answer -= i
        else:
            answer += i
    return answer

---

문제 설명

1) 기본 설명

- 프로그래머스에서 제공하는 기본 함수는 다음과 같습니다.

def solution(left, right):
    answer = 0
    return answer

---

2) 문제 다가가기

(1) left부터 right까지의 모든 수를 탐색하며 약수의 개수를 구한다.

(2) 약수의 개수가 짝수개라면 n을 더하고, 홀수개라면 더한다.

(추가) 모든 제곱수의 약수의 개수는 홀수이다. (다른 사람의 코드 확인)

---

3) 코드 설명

(1) dividor 함수 구현

def dividor(n):
    result = len([i for i in range(1, n+1) if not n%i])
    return -n if result%2 else n

- for문의 내포를 이용하여 약수의 개수를 구했습니다.

- i가 n으로 나누어떨어진다면 result에 더합니다.

    -> Python에서 0이 아닌 수는 True로 판별됩니다.

    -> n%i == 0 -> False 입니다. 이를 not 을 이용하여 표현했습니다.

- 만약 result의 길이가 홀수라면 -n을 , result의 길이가 짝수개라면 n을 return 합니다.

---

(2) dividor 함수 호출

def solution(left, right):
    result = 0
    for i in range(left, right + 1):
        result += dividor(i)
    return result

- for i in range(3)이라면, i = 0, 1, 2입니다.

    -> for i in range(1, 3)이라면 i = 1, 2입니다.

    -> 우리는 left부터 right까지 호출해야하기 때문에  for i in range(left, rigth+1) 을 실행해야합니다.

- return 받은 결과값을 모두 더해 반환하면 끝입니다 !

---

3) 다른 사람의 코드 설명

- 모든 제곱수의 약수는 홀수입니다.

    -> 25 = 1, 5, 25

    -> 9 = 1, 3, 9

def solution(left, right):
    answer = 0
    for i in range(left,right+1):
        if int(i**0.5)==i**0.5:
            answer -= i
        else:
            answer += i
    return answer

- **은 제곱수를 구하는 연산자입니다.

    -> n ** 2 -> n*n 입니다.

    -> n ** (1/2)가 루트를 표현하는 것 아시죠 ? -> n ** 0.5로 루트 값을 구할 수 있습니다.

        -> math.sqrt와 같은 값을 구하는 것이겠죠!?

- int(i**0.5) == i**0.5 -> 제곱수라면 i를 빼고, 아니라면 i를 더합니다.

- if else 문을 사용했으니 당연히 삼항연산자를 사용할 수 있습니다.

---

def solution(left, right):
    answer = 0
    for i in range(left, right+1):
        answer = answer - i if int(i**0.5) == i**0.5 else answer + i
    return answer

제곱수라면 answer - i (약수의 개수가 홀수), 제곱수가 아니라면 answer + i (약수의 개수가 짝수)

---

수학적 지식을 이용해 더 좋은 로직을 만들 수 있다는 것을 알게 되었습니다.

 

➕제 깃허브 들어오시면, 설명은 없지만 다른 문제들의 코드를 볼 수 있습니다.

GitHub - JIWON1923/Algorithm: studying algorithm with python